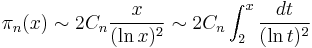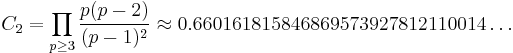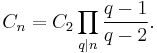Polignac's conjecture

In number theory, Polignac's conjecture was made by Alphonse de Polignac in 1849 and states:

For any positive even number n, there are infinitely many prime gaps of size n. In other words: There are infinitely many cases of two consecutive prime numbers with difference n.[1]

The conjecture has not been proven or disproven for any value of n.

For n = 2, it is the twin prime conjecture. For n = 4, it says there are infinitely many cousin primes (p, p + 4). For n = 6, it says there are infinitely many sexy primes (p, p + 6) with no prime between p and p + 6.

Dickson's conjecture generalizes Polignac's conjecture to cover all prime constellations; the Bateman–Horn conjecture gives conjectured asymptotic densities.

Conjectured density

Let 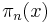\pi_n(x) for even n be the number of prime gaps of size n below x.

The first Hardy–Littlewood conjecture says the asymptotic density is of form

\pi_n(x) \sim 2 C_n \frac{x}{(\ln x)^2} \sim 2 C_n \int_2^x {dt \over (\ln t)^2}

where Cn is a function of n, and 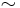\sim means that the quotient of two expressions tends to 1 as x approaches infinity.

C2 is the twin prime constant

C_2 = \prod_{p\ge 3} \frac{p(p-2)}{(p-1)^2} \approx 0.66016 18158 46869 57392 78121 10014\dots

where the product extends over all prime numbers p ≥ 3.

Cn is C2 multiplied by a number which depends on the odd prime factors q of n:

C_n = C_2 \prod_{q|n} \frac{q-1}{q-2}.

For example, C4 = C2 and C6 = 2C2. Twin primes have the same conjectured density as cousin primes, and half that of sexy primes.

Note that each odd prime factor q of n increases the conjectured density compared to twin primes by a factor of 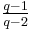\tfrac{q-1}{q-2}. A heuristic argument follows. It relies on some unproven assumptions so the conclusion remains a conjecture. The chance of a random odd prime q dividing either a or a + 2 in a random "potential" twin prime pair is 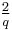\tfrac{2}{q}, since q divides 1 of the q numbers from a to a + q − 1. Now assume q divides n and consider a potential prime pair (a, a + n). q divides a + n if and only if q divides a, and the chance of that is 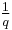\tfrac{1}{q}. The chance of (a, a + n) being free from the factor q, divided by the chance that (a, a + 2) is free from q, then becomes 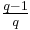\tfrac{q-1}{q} divided by 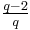\tfrac{q-2}{q}. This equals 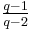\tfrac{q-1}{q-2} which transfers to the conjectured prime density. In the case of n = 6, the argument simplifies to: If a is a random number then 3 has chance 2/3 of dividing a or a + 2, but only chance 1/3 of dividing a and a + 6, so the latter pair is conjectured twice as likely to both be prime.

References

  1. ^ Tattersall, J.J. (2005), Elementary number theory in nine chapters, Cambridge University Press, ISBN 978-0-521-85014-8, http://books.google.de/books?id=QGgLbf2oFUYC , p. 112